Теория и практика межпланетных перелетов. Часть 4. Выход на орбиту с заданной ориентацией в пространстве
Ноги этого вопроса растут из игровых задач. Например в карьере есть контракты типа "запустить спутник Кербина с заданными параметрами орбиты". И приводятся параметры орбиты: наклонение, долгота восходящего узла, аргумент перицентра и высота перицентра и апоцентра над поверхностью планеты.
Кроме того, ну мало кто из опытных и не очень игроков не летал на Минмус. Орбита Минмуса, в отличие от Мун, наклонена к плоскости орбиты Кербина (к эклиптике!) под углом 6 градусов. А долгота восходящего узла этой орбиты - 78 градусов.
Выходя на экваториальную орбиту довольно сложно спланировать экономный трансфер к Минмусу, даже используя MechJeb. Никто не говорит, что это нереально, но затраты выйдут довольно серьезыми, да и поймать нужную точкность для орбиты подхода к спутнику довольно тяжело.
Очевидное решение - выровнять плоскости орбит. Это можно сделать и руками, можно и MechJeb-ом. Но на круговой орбите в 80 км это потребует около 240 м/с дельты. А если для межпланетного трансфера требуется большее наклонение опорной орбиты? Ведь старт к планетам не всегда можно произвести из экваториальной плоскости.
Другое решение - сразу выйти на орбиту с нужной ориентацией. Это серьезно съэкономит топливо - заставим первые ступени РН не только забросить нас на нужную высоту, но и сразу построим нужную орбиту.
Другой вопрос - где брать данные о параметрах текущей орбиты? MechJeb и VOID показывают наклонение, но не долготу узлов. И вот тут нам на помощь приходит точный расчет.
1. Системы координат, отсчета времени и механика вращения небесных тел в KSP
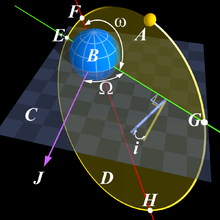
Чтобы ориентироваться в пространстве, надо знать, как в каждый интересующий нас момент времени расположена планета, с которой мы стратуем. Вот так например, выглядит наша планета Земля

Горизонтальная плоскость на рисунке - плоскость эклиптики. Плоскость, наклоненная под углом delta - плоскость экватора Земли. Пересекаются они по прямой, направленной на точку весеннего равноденствия. Именно линия пересечения экватора Земли с плоскостью её орбиты и есть то направление, откуда в Солнечной системе отсчитываются все угловые координаты. Прямая NS - ось вращения Земли. Соответственно N - северный полюс, а S - южный. Если пренебречь прецессией и нутацией, то ось вращения Земли движется в пространстве поступательно и не меняет своей ориентации в пространстве. А линия углов экватора всегда смотрит в сторону точки весеннего равноденствия. Дуга NAS идущая через полюса есть нулевой меридиан Гринвича, относительно которого отсчитываются на Земле все долготы. Поскольку Земля вращается, то нулевой меридиан, в каждый момент времени повернут относительно точки весеннего равноденствия на некоторый угол t, называемый часовым углом. Этот угол характеризует так называемое звездное время.
Наконец положение нашего космодрома M определяется широтой - дуга BM (угол phi), и долготой - дуга AB (угол lambda).
Если говорить о других планетах Солнечной системы, то линия узлов их экваториальных плоскостей не направлена на точку весеннего равноденствия, а составляет с ней некоторый угол Omega, так, как показано на следующем чертеже.

Здесь формулы для расчета наклонения орбиты к плоскости эклиптики и долготы её восходящего узла придется воспользоваться довольно громоздкими формулами.
Что касается Кербальской системы, то тут пока что всё предельно просто - экваториальные плоскости всех планет лежат в плоскости эклиптики и всё выглядит так

Красной линией показана трасса орбиты на поверхности планеты. Очевидно, что положение узла орбиты зависит от того, на какой угол t повернута планета в момент запуска, а так же от долготы места запуска. Красный вектор vk - фактическая круговая скорость движения по орбите, получаемая при запуске (ограничимся рассмотрением круговых орбит). Зеленый вектор vs - скорость точки поверхности планеты, из которой производится запуск. Да-да, когда ракета отрывается от старта, она уже имеет орбитальную скорость равную окружной скорости вращения планеты в данном месте. Для KSC эта скорость примерно 174 м/с. Именно поэтому ракеты стараются пускать на восток, дабы получить халявную дельту. Эта скорость зависит от широты места старта phi

Здесь: omega - угловая скорость вращения планеты; R - экваториальный радиус планеты. Угловая скорость планеты легко вычисляется через известный параметр - период вращения планеты вокруг своей оси Tr

Кроме того, космодром лучше располагать поближе к экватору по двум причинам. Первая - большая окружная скорость из-за меньшей широты. Вторая - больший диапазон достижимых наклонений орбиты. Чтобы понять, почему так происходит, следует ответить на вопрос, а чем вообще определяется наклонение орбиты? Оно определяется азимутом запуска Az. Его можно рассчитать, зная широту места старта и желаемое наклонение, а так же требуемую орбитальную скорость


здесь у нас: i - желаемое наклонение орбиты, а угол обозначенный закорюкой с именем "кси" - азимут старта, который требовался бы, если бы планета не вращалась. Напомню, что азимутом называется угол между направлением нашего движения и касательной к меридиану, направленной в сторону севера. В KSP этот параметр называется истинным курсом - HDG.
Из второй формулы видно важную вещь - синус не может быть более единицы и менее минус единицы. А значит

откуда следует, что

то есть
При запуске с поверхности планеты, наклонение орбиты не может быть меньше, чем широта точки старта
Поэтому космодром лучше располагать на экваторе. А вот, например, для Байконура нельзя получить наклонение менее 45 градусов, ибо такова его широта. Ограничения на район падения ступеней увеличивает этот предел до 51 градуса. Американцам в этом смысле проще - 28 градусов широты и океан, куда ступени могут спокойно падать. На Кербине ещё проще - широта KSC составляет 6 минут южной широты, то есть доступны наклонения до 6 угловых минут.
Программное поддержания азимута в процессе выведения ракеты даст нам требуемое наклонение орбиты. И тут есть сложность - азимут будет изменятся, ведь меридианы искривляются по мере того как мы поднимаемся в более высокие широты. Поэтому, для точного выведения требуется периодически пересчитывать азимут, меняя курс.
Что касается долготы узла, то нам необходимо вычислить, на какой угол должен быть повернут космодром относительно точки весеннего равноденствия, чтобы обеспечивался требуемая долгота восходящего узла. Этот угол лежит в пределах от 0 до 360 градусов и его можно вычислить по формулам


Угол поворота точки старта связан с долготой места старта и углом поворота планеты (звездным временем)

Откуда мы найдем требуемые в момент старта угол поворота планеты

Подобрав время запуска, и соблюдая азимут запуска мы получим нужную нам орбиту.
Такова теория. Теперь рассмотрим практику
2. Выход на орбиту для полета на Минмус
Параметры орбиты Минмуса таковы: наклонение - 6 градусов, долгота восходящего узла - 78 градусов. Координаты точки запуска: широта минус 6 минут 10 секунд, долгота - минус 74 градуса 34 минуты 31 секунда. Исходя их этих формул рассчитаем азимут старта и угол поворота планеты, учитывая, что скорость вращения Кербина на данной широте - 174.53 м/с, а орбитальная скорость на высоте 80 км равна 2279 м/с. Воспользовавшись формулами получим следующие данные

У нас есть азимут пуска - 83.50 градуса. Хорошо. Нам так же стало известно, что нулевой меридиан Кербина должн быть повернут на угол 153.54 градуса. Когда нам стартовать? Это зависит от текущей даты. Допустим у нас 31 год 1 день 0 часов 0 минут 0 секунд. Переведем это время в секунды T = 276048000 секунд, прошедших от эпохи UT 0 (1 год 1 день 0 часов 0 минут 0 секунд). Расчитаем угол поворота Кербина в интересующую нас дату

Здесь - Tr = 21599.912 секунд - период вращения Кербина вокруг своей оси. Внимание: не 21600, а именно 21599.912!. Имеются в виду звездные сутки Кербина, его фактический период вращения относительно инерциальной системы отсчета. Взяв 21600 на больших промежутках времени мы получим большую ошибку.
Угол t0 в KSP называется initialRotation - начальный угол поворота планеты в эпоху UT 0. Для Кербина он равен 90 градусам, для Ив - 0 градусов, для Дюны - 230 градусов.
Если мы посчитаем угол tc, то получим значение много превышающее 360 градусов. Ещё бы, за 30 лет планета совершит не один оборот. Отбросим целое число оборотов, и получим угол поворота

равный 108.74 градуса. За 30 лет Кербин сделает 12780 оборотов вокруг оси и довернется ещё на 108.74 градуса.
Итого, выходит нам нужно подождать ещё некоторое время, когда Кербин довернется на dt = 153.54 - 108.74 = 44.8 градуса. За какое время он это сделает? Если 360 градусов занимает 21599.912 секунд, то с 44.8 мы управимся за 44 минуты 47 секунд. Итак, дата старта 31 год 1 день 0 часов 44 минуты 47 секунд. Проверим что получится.
3. Выход на расчетную орбиту
Запуская KSP, ставим дату 31 год 1 день 0 часов 0 минут 0 секунд. Это удобно сделать с помощью HyperEdit. Теперь вопрос - чем выводить? Автопилот мехджеба не подходит - он отвратительно делает наклонение орбиты. Видимо он не учитывает ни вращения планеты, ни изменения азимута в процессе выведения. Так что используем Smart S.A.S от мехджеба, на которой выставим курс 83.5 градуса и тангаж в 90 градусов. Наклонение орбиты будем контролировать по утилите Orbit Info. Стартуем в 0:44:47 по кербальскому времени.

Теперь рулим по тангажу и одновременно следим за ступенями и наклонением орбиты. Когда оно достигает 6 градусов - отсекаем тягу. Сразу после отсечки программируем циркуляризацию орбиты.

Такой подход - вынужденная мера и неверен технически, но точного автопилота по наклонению у нас нет. После того как отработает циркуляризация идем в карту, выбираем Минмус в качестве цели и смотрим плоскости орбит

Отклонение от плоскости - 0.3 градуса. При необходимости это проще нивелировать, чем все 6 градусов. Таким образом мы достигли цели - вышли на орбиту, лежащую в плоскости орбиты Минмуса и можем строить трансфер.
Заключение
Что мы выяснили? Что азимут запуска влияет на наклонение орбиты, а время запуска определяет долготу её узлов. Надеюсь читателю это пригодится.
P.S.: Я научил "Звездочета" определять дату запуска. Для межпланетного перелета рассчитывается наклонение опорной орбиты, дата запуска и азимут запуска. Новую версию программы можно получить вот тут. Исходники по прежнему доступны в официальном репозитории проекта.

Hello there!
Дорогой Гость, чат доступен только для зарегистрированных пользователей.
Последние комментарии
ОБНОВЛЕНИЕ! Параллельный импорт EVE Raymarched Volumetrics версия "Иду на грозу" (июль2024)
Как сделать облака и на других планетах по типу Евы или джула. И как сделать так чтобы на дюне были
Kerbal Space Program (KSP) 1.12.5 скачать - "On Final Approach" + DLC
тут хотя бы не троян?
[РУСИФИКАТОР] KSP 1.0.x
Спасибо огромное на финальной версий 1.12.5 всё переведено идеально
Параллельный импорт EVE Raymarched Volumetrics - RSS "Облака планеты Земля"
я видеокарта gtx660 мод потянет?

ОБНОВЛЕНИЕ! Параллельный импорт EVE Raymarched Volumetrics версия "Иду на грозу" (июль2024)
доброго времени суток там случайно новых версий за полгода не вышло?

Все комментарии..
Полный список последних комментариев
Последние сообщения с форума

Все сообщения..
Полный список последних сообщений
Loading...
Нашли ошибку?
Вы можете сообщить об этом администрации.
Выделив текст нажмите Ctrl+Alt