KerboScript в примерах и задачах. Часть 4. Разбираемся в орбитах.
В предыдущих частях рассмотрены базовые функции для вывода аппарата на орбиту и манёвров в пределах экваториальной плоскости. Настало время выйти в трёхмерный мир.
Замечание. Далее в тексте будет встречаться векторное произведение. Во всех формулах будет предполагаться, что его направление определяется правилом правого винта, как обычно принято в физике. В примерах кода всё ровно наоборот, потому что внутри игры используется левосторонняя система координат.
Состояние материальной точки в классической механике, как известно, полностью описывается шестью параметрами - тремя компонентами радиус-вектора и тремя компонентами вектора скорости. Однако в случае свободного орбитального движения такое описание не очень удобно, поскольку и координаты, и скорость меняются со временем.
Вместо этого в орбитальной механике традиционно используется другое представление движения, которое тоже требует шесть параметров (необходимость взаимно однозначного преобразования к координатам и скорости никто не отменял), но меняется из них только один, отвечающий за положение на орбите. Остальными пять описывают собственно орбита. Два параметра требуются для описания её формы, три - для описания положения в пространстве.
Эти 6 параметров называются кеплеровыми элементами орбиты. Вот список:
- большая полуось (Semi-Major Axis или SMA)
- эксцентриситет (Eccentricity)
- долгота восходящего узла (Longitude of Ascending Node или LAN)
- наклонение (Inclination)
- аргумент перицентра (Argument of Periapsis)
- средняя аномалия (Mean Anomaly)
Как видно, при свободном движении точки по орбите меняется только средняя аномалия, причём по простому линейному закону. Все остальные параметры являются инвариантами орбитального движения.
Орбита, согласно первому закону Кеплера, представляет собой коническое сечение, в фокусе которого находится центр притяжения. К коническим сечениям относятся прямые, окружности, эллипсы, параболы и гиперболы. Тип конического сечения однозначно определяется величиной полной механической энергией единицы массы тела на орбите:
где v - орбитальная скорость тела, R - расстояние до центра притяжения (центра небесного тела), μ - гравитационный параметр притягивающего тела (произведение массы на гравитационную постоянную).
В отсутствие внешних сил механическая энергия тела на орбите сохраняется, значит, величины ε < 0 соответствует замкнутым траекториям - эллипсам (поскольку v2/2 всегда больше 0, то при отрицательной энергии расстояние до центра не может быть сколь угодно большим), ε = 0 соответствует параболическим траекториям (тело на бесконечности имеет нулевую скорость), ε > 0 соотвествует гиперболическим траекториям (тело имеет на бесконечности ненулевую скорость, и траектория на большом удалении от центра стремится к прямой линии).
Кроме того, из законов Ньютона можно вывести, что удельная механическая энергия взаимно однозначно определяет величину большой полуоси орбиты a:
(заметим, что для гиперболических орбит в этом случае величина большой полуоси считается отрицательной). Таким образом, удельная энергия определяет тип и размер орбиты. Кроме того, большая полуось однозначно определяет период орбиты:
Форма орбиты характеризуется эксцентриситетом, который равен
где c - половина расстояния между фокусами эллипса или гиперболы. Для окружности e = 0 (оба фокуса совпадают), для эллипса 0 < e < 1, для гиперболы e > 1, для параболы e = 1.
Эксцентриситет определяется удельной энергией ε и удельным моментом импульса h = [r×v] по формуле

В некоторых случаях может быть удобнее рассматривать эксцентриситет как вектор:

Замечательное свойство этого вектора состоит в том, что он направлен от апоцентра орбиты к перицентру.

Зная геометрические соотношения, можно вывести формулы для вычисления малой полуоси b, расстояний от фокуса до перицентра RPe и до апоцентра RAp через большую полуось и эксцентриситет, и наоборот:

В случае гиперболической орбиты b - это прицельный параметр, т.е. расстояние от центра притяжения до асимптот гиперболы. Апоцентр гиперболической орбиты считается отрицательным, так чтобы RAp + RPe = 2a.
Далее будут рассматриваться эллиптические орбиты, для гиперболических всё практически то же самое, параболы и окружности, как вырожденные случаи, рассмотрены не будут.
Ориентация орбиты в пространстве определяется тремя углами: долготой восходящего узла, наклонением и аргументом перицентра. По сути, они соответствуют трём углам Эйлера.
Долгота восходящего узла, наклонение и аргумент перицентра вовсю встречаются в контрактах на спутники.

Также их можно увидеть при задании орбиты через чит-меню.

Для определения этих углов необходимы следующие понятия:
- базовая плоскость - плоскость, проходящая через центр притяжения, для которой задан вектор нормали. Обычно за базовую берётся экваториальная плоскость центрального тела, нормаль направлена на север, т.е. в направлении вектора момента импульса суточного вращения.
- узлы орбиты (orbital nodes) - точки, в которых орбита пересекает базовую плоскость. В восходящем узле (Ascending Node или AN) вектор орбитальной скорости имеет положительную проекцию на нормаль к базовой плоскости (экватор пересекается с юга на север), в нисходящем узле (Descending Node или DN) - отрицательную (экватор пересекается с севера на юг).
- линия узлов - прямая, соединяющая нисходящий и восходящий узел. По линии узлов плоскость орбиты пересекается с экваториальной плоскостью. Поскольку центр гравитирующей планеты лежит как в базовой плоскости, так и в плоскости орбиты, линия узлов проходит через этот центр. Линия узлов считается направленной от центра к восходящему узлу.
- апсиды - общее название для перицентра и апоцентра.
- линия апсид - прямая, содержащая большую полуось эллипса или ось симметрии незамкнутой орбиты. Очевидно, проходит через гравитационный центр. Линия апсид считается направленной от центра к перицентру орбиты.
- нормаль к орбите - прямая, проходящая через центр гравитации перпендикулярно плоскости орбиты. Считается направленной в ту же сторону, что и удельный момент импульса h.
Для однозначного определения ориентации орбиты в пространстве достаточно знать направления линии узлов, линии апсид и нормали к орбите. Для задания этих направлений вводится сферическая система координат, у которой зенитная ось Z соответствует нормали к базовой плоскости (если в качестве базовой взята плоскость экватора - то ось Z смотрит на север), а азимутальная ось X, задающая нулевой небесный меридиан - от центра планеты вдоль произвольно выбранного фиксированного вектора (в земной астрономии это направление на точку весеннего равноденствия). В этом случае:
- долгота восходящего узла - угол между осью X и направлением на восходящий угол орбиты, отсчитываемый против часовой стрелки
- наклонение орбиты - угол между осью Z и вектором нормали к орбите (он же угол между базовой плоскостью и ориентированной плоскостью орбиты)
- аргумент перицентра - угол в плоскости орбиты, отсчитываемый от направления на восходящий узел (линии узлов) к направлению на перицентр (линии апсид) в направлении орбитального движения.
Стандартная картинка для иллюстрации этих углов:

Как видно из рисунка 4, узлы, наклонение и аргумент перицентра можно ввести относительно любой базовой плоскости - в частности, как известно, в игре показываются узлы относительно плоскости орбиты аппарата или тела, указанного в качестве цели.
Теперь, после краткого объяснения теории, переходим к получению элементов орбиты из kOS.
Тип данных ORBIT позволяет получить сведения об орбите. По умолчанию у любого объекта типа ORBITABLE (к ним относятся все крафты и небесные тела) имеется суффикс ORBIT, который возвращает орбиту этого объекта. Большая часть суффиксов типа ORBIT как раз и возвращает геометрические характеристики орбиты и положения тела на ней:
Заметим, что средняя аномалия даётся на эпоху, т.е. на абсолютное время 0 (полночь первого дня по игровому календарю). Средняя аномалия в данный момент равна по определению:
M = M0 + t/T×360°
Оставшиеся суффиксы типа ORBIT нужны для того, чтобы понять, куда орбита ведёт дальше:
Суффикс TRANSITION может принимать следующие значения:
"FINAL" - если орбита стабильна, т.е. в ближайшее время перехода в другую сферу влияния не предвидится
"ENCOUNTER" - ожидается переход в сферу влияния спутника текущего центрального тела (пример: орбита вокруг Дюны, пересекает сферу действия Айка)
"ESCAPE" - ожидается выход в сферу действия более крупного тела (пример: орбита вокруг Минмуса, ожидается уход в сферу действия Кербина)
"MANEUVER" - впереди на орбите установлен манёвр
Примеры использования типа ORBIT:
Последний шаг, необходимый для полного знания об орбите, помимо орбитальных элементов - это узнать направление оси X, от которой отсчитывается долгота восходящего узла (направление полярной оси уже известно - оно имеет вид V(0,1,0) ). Это направление доступно из kOS как SOLARPRIMEVECTOR:
В качестве упражнения, напишем несколько полезных функций для расчёта орбитальных направлений.
1. Вектор нормали к орбите. Определяется направлением момента импульса [r×v].
2. Направление линии узлов. Поскольку линия узлов лежит как в экваториальной плоскости, так и в плоскости орбиты, она перпендикулярна полярной оси планеты (V(0,1,0)) и нормали к орбите, т.е. направлена вдоль векторного произведения этих векторов. Направление на восходящий узел соответствует произведению [North×n] (см. рис. 4).
3. Линия узлов одной орбиты относительно другой. Считается аналогично экваториальной линии узлов, только вместо оси, направленной на север, необходимо взять нормаль к орбите, принятой за базовую.
4. Взаимное наклонение двух орбит.
Очевидно, равно углу между нормалями к орбитам:
5. Линия апсид. Она сонаправлена с вектором эксцентриситета.
6. Нормаль и линия узлов орбиты по заданным величинам долготы восходящего узла и наклонения.
Смотрим рисунок 4. Линия узлов получается поворотом оси X вокруг оси Z на долготу восходящего узла, нормаль получается поворотом оси Z вокруг линии узлов на наклонение. Воспользуемся функцией ANGLEAXIS для направлений, чтобы выполнить эти повороты. А поскольку линия узлов и нормаль всегда перпендикулярны, их удобно хранить в одной переменной направления, например, линию узлов в поле FOREVECTOR, нормаль в поле UPVECTOR.
При необходимости, можно получить и линию апсид, повернув линию узлов вокруг нормали на аргумент перицентра.
Теперь используем эти функции для поворота круговой орбиты другую плоскость, задаваемую долготой восходящего узла и наклонением.
Начальную орбиту будем считать круговой, поворот будет производиться в один прожиг, причём так, чтобы конечная орбита также была круговой. Для простоты расчёта, манёвр ставится в восходящем узле, а не в ближайшем по времени.
Вектор скорости при манёвре следует повернуть на угол i по часовой стрелке вокруг радиус-вектора в восходящем узле (см. рис. 5). Манёвр имеет компоненты в направлении нормали к орбите и вектора орбитальной скорости.

Если рассматривать всё в осях (Radial, Normal, Prograde) относительно исходной орбитальной скорости, то исходный вектор орбитальной скорости имеет координаты (0, 0, V0), новый - (0, -V0sin i, V0cos i). Следовательно, вектор ΔV имеет компоненты (0, -V0sin i, V0(cos i - 1) ).
Замечание. При большом взаимном наклонении орбит может быть выгоднее делать поворот "через бесконечность", т.е. сначала поднять апоцентр к границе сферы действия, сменить наклонение в апоцентре, затем в перицентре опять опустить апоцентр. Здесь приводится простой скрипт, который эффективность манёвра не анализирует.
Более сложный пример - переход на более высокую круговую орбиту в другой плоскости. В этом случае выгодно сначала в одном из узлов поднять апоцентр без изменения плоскости (в итоге получится орбита с аргументом перицентра 0° или 180°), затем в апоцентре сделать комбинацию скругления орбиты и поворота в новую плоскость.
Манёвр подъёма апоцентра предлагаю рассчитать самостоятельно, приведу здесь только функцию комбинированного манёвра скругления и поворота орбиты в апоцентре.

Будем считать, что первый манёвр произведён в нисходящем узле, т.е. апоцентр попадает в восходящий узел (аргумент перицентра 180°). По схеме на рис. 6 видим:
V1,PRG = V1 cos i
V1,NRM = -V1 sin i
ΔV = (0, -V1sin i, V1cos i - V0 )
На основе этого пишем функцию:
Естественно, если нужно перейти на более низкую орбиту в другой плоскости, то порядок действий должен быть обратным - сначала опускается перицентр с одновременным поворотом плоскости, затем орбита скругляется в перицентре.
На этом завершаю настоящую часть руководства. Далее будет рассмотрен вопрос взлёта с поверхности сразу в нужную плоскость.
Замечание. Далее в тексте будет встречаться векторное произведение. Во всех формулах будет предполагаться, что его направление определяется правилом правого винта, как обычно принято в физике. В примерах кода всё ровно наоборот, потому что внутри игры используется левосторонняя система координат.
Состояние материальной точки в классической механике, как известно, полностью описывается шестью параметрами - тремя компонентами радиус-вектора и тремя компонентами вектора скорости. Однако в случае свободного орбитального движения такое описание не очень удобно, поскольку и координаты, и скорость меняются со временем.
Вместо этого в орбитальной механике традиционно используется другое представление движения, которое тоже требует шесть параметров (необходимость взаимно однозначного преобразования к координатам и скорости никто не отменял), но меняется из них только один, отвечающий за положение на орбите. Остальными пять описывают собственно орбита. Два параметра требуются для описания её формы, три - для описания положения в пространстве.
Эти 6 параметров называются кеплеровыми элементами орбиты. Вот список:
- большая полуось (Semi-Major Axis или SMA)
- эксцентриситет (Eccentricity)
- долгота восходящего узла (Longitude of Ascending Node или LAN)
- наклонение (Inclination)
- аргумент перицентра (Argument of Periapsis)
- средняя аномалия (Mean Anomaly)
Как видно, при свободном движении точки по орбите меняется только средняя аномалия, причём по простому линейному закону. Все остальные параметры являются инвариантами орбитального движения.
Орбита, согласно первому закону Кеплера, представляет собой коническое сечение, в фокусе которого находится центр притяжения. К коническим сечениям относятся прямые, окружности, эллипсы, параболы и гиперболы. Тип конического сечения однозначно определяется величиной полной механической энергией единицы массы тела на орбите:
ε = v2/2 - μ/R,
где v - орбитальная скорость тела, R - расстояние до центра притяжения (центра небесного тела), μ - гравитационный параметр притягивающего тела (произведение массы на гравитационную постоянную).
В отсутствие внешних сил механическая энергия тела на орбите сохраняется, значит, величины ε < 0 соответствует замкнутым траекториям - эллипсам (поскольку v2/2 всегда больше 0, то при отрицательной энергии расстояние до центра не может быть сколь угодно большим), ε = 0 соответствует параболическим траекториям (тело на бесконечности имеет нулевую скорость), ε > 0 соотвествует гиперболическим траекториям (тело имеет на бесконечности ненулевую скорость, и траектория на большом удалении от центра стремится к прямой линии).
Кроме того, из законов Ньютона можно вывести, что удельная механическая энергия взаимно однозначно определяет величину большой полуоси орбиты a:
a = μ/(2ε)
(заметим, что для гиперболических орбит в этом случае величина большой полуоси считается отрицательной). Таким образом, удельная энергия определяет тип и размер орбиты. Кроме того, большая полуось однозначно определяет период орбиты:
T2 = (2π)2a3/μ
Форма орбиты характеризуется эксцентриситетом, который равен
e = |c/a|,
где c - половина расстояния между фокусами эллипса или гиперболы. Для окружности e = 0 (оба фокуса совпадают), для эллипса 0 < e < 1, для гиперболы e > 1, для параболы e = 1.
Эксцентриситет определяется удельной энергией ε и удельным моментом импульса h = [r×v] по формуле

В некоторых случаях может быть удобнее рассматривать эксцентриситет как вектор:

Замечательное свойство этого вектора состоит в том, что он направлен от апоцентра орбиты к перицентру.

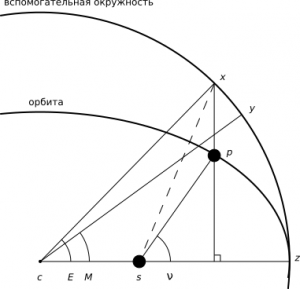
Рисунок 1. Эллипсы с одинаковой величиной большой полуоси и разным эксцентриситетом. Крестиками показаны положения фокусов (второй фокус расположен симметрично с левой стороны).
Зная геометрические соотношения, можно вывести формулы для вычисления малой полуоси b, расстояний от фокуса до перицентра RPe и до апоцентра RAp через большую полуось и эксцентриситет, и наоборот:

В случае гиперболической орбиты b - это прицельный параметр, т.е. расстояние от центра притяжения до асимптот гиперболы. Апоцентр гиперболической орбиты считается отрицательным, так чтобы RAp + RPe = 2a.
Далее будут рассматриваться эллиптические орбиты, для гиперболических всё практически то же самое, параболы и окружности, как вырожденные случаи, рассмотрены не будут.
Ориентация орбиты в пространстве определяется тремя углами: долготой восходящего узла, наклонением и аргументом перицентра. По сути, они соответствуют трём углам Эйлера.
Долгота восходящего узла, наклонение и аргумент перицентра вовсю встречаются в контрактах на спутники.

Рисунок 2. Типичное описание орбиты для контракта
Также их можно увидеть при задании орбиты через чит-меню.

Рисунок 3. Меню установки орбиты. Есть поля для установки большой полуоси, эксцентриситета, наклонения, средней аномалии (MNA), долготы восходящего узла (LAN) и аргумента перицентра (LPE).
Для определения этих углов необходимы следующие понятия:
- базовая плоскость - плоскость, проходящая через центр притяжения, для которой задан вектор нормали. Обычно за базовую берётся экваториальная плоскость центрального тела, нормаль направлена на север, т.е. в направлении вектора момента импульса суточного вращения.
- узлы орбиты (orbital nodes) - точки, в которых орбита пересекает базовую плоскость. В восходящем узле (Ascending Node или AN) вектор орбитальной скорости имеет положительную проекцию на нормаль к базовой плоскости (экватор пересекается с юга на север), в нисходящем узле (Descending Node или DN) - отрицательную (экватор пересекается с севера на юг).
- линия узлов - прямая, соединяющая нисходящий и восходящий узел. По линии узлов плоскость орбиты пересекается с экваториальной плоскостью. Поскольку центр гравитирующей планеты лежит как в базовой плоскости, так и в плоскости орбиты, линия узлов проходит через этот центр. Линия узлов считается направленной от центра к восходящему узлу.
- апсиды - общее название для перицентра и апоцентра.
- линия апсид - прямая, содержащая большую полуось эллипса или ось симметрии незамкнутой орбиты. Очевидно, проходит через гравитационный центр. Линия апсид считается направленной от центра к перицентру орбиты.
- нормаль к орбите - прямая, проходящая через центр гравитации перпендикулярно плоскости орбиты. Считается направленной в ту же сторону, что и удельный момент импульса h.
Для однозначного определения ориентации орбиты в пространстве достаточно знать направления линии узлов, линии апсид и нормали к орбите. Для задания этих направлений вводится сферическая система координат, у которой зенитная ось Z соответствует нормали к базовой плоскости (если в качестве базовой взята плоскость экватора - то ось Z смотрит на север), а азимутальная ось X, задающая нулевой небесный меридиан - от центра планеты вдоль произвольно выбранного фиксированного вектора (в земной астрономии это направление на точку весеннего равноденствия). В этом случае:
- долгота восходящего узла - угол между осью X и направлением на восходящий угол орбиты, отсчитываемый против часовой стрелки
- наклонение орбиты - угол между осью Z и вектором нормали к орбите (он же угол между базовой плоскостью и ориентированной плоскостью орбиты)
- аргумент перицентра - угол в плоскости орбиты, отсчитываемый от направления на восходящий узел (линии узлов) к направлению на перицентр (линии апсид) в направлении орбитального движения.
Стандартная картинка для иллюстрации этих углов:

Рисунок 4. Ориентация орбиты в пространстве.
Как видно из рисунка 4, узлы, наклонение и аргумент перицентра можно ввести относительно любой базовой плоскости - в частности, как известно, в игре показываются узлы относительно плоскости орбиты аппарата или тела, указанного в качестве цели.
Теперь, после краткого объяснения теории, переходим к получению элементов орбиты из kOS.
Тип данных ORBIT позволяет получить сведения об орбите. По умолчанию у любого объекта типа ORBITABLE (к ним относятся все крафты и небесные тела) имеется суффикс ORBIT, который возвращает орбиту этого объекта. Большая часть суффиксов типа ORBIT как раз и возвращает геометрические характеристики орбиты и положения тела на ней:
APOAPSIS // высота апоцентра в метрах (над уровнем моря)
PERIAPSIS // высота перицентра в метрах
BODY // возвращает центральное тело (тип данных BODY)
PERIOD // период орбиты в секундах
INCLINATION // наклонение в градусах
ECCENTRICITY // эксцентриситет
SEMIMAJORAXIS // большая полуось в метрах
SEMIMINORAXIS // малая полуось в метрах
LAN // долгота восходящего узла в градусах
ARGUMENTOFPERIAPSIS // аргумент перицентра в градусах
TRUEANOMALY // истинная аномалия в градусах
MEANANOMALYATEPOCH // средняя аномалия в градусах
POSITION // текущее положение (тип VECTOR)
VELOCITY // текущая скорость (тип ORBITABLEVELOCITY)
Заметим, что средняя аномалия даётся на эпоху, т.е. на абсолютное время 0 (полночь первого дня по игровому календарю). Средняя аномалия в данный момент равна по определению:
M = M0 + t/T×360°
Оставшиеся суффиксы типа ORBIT нужны для того, чтобы понять, куда орбита ведёт дальше:
TRANSITION // что будет с орбитой далее (строка)
NEXTPATCH // орбита после перехода в новую сферу действия (тип ORBIT)
NEXTPATCHETA // время в секундах до перехода в новую сферу действия
HASNEXTPATCH // наличие перехода (BOOLEAN)
Суффикс TRANSITION может принимать следующие значения:
"FINAL" - если орбита стабильна, т.е. в ближайшее время перехода в другую сферу влияния не предвидится
"ENCOUNTER" - ожидается переход в сферу влияния спутника текущего центрального тела (пример: орбита вокруг Дюны, пересекает сферу действия Айка)
"ESCAPE" - ожидается выход в сферу действия более крупного тела (пример: орбита вокруг Минмуса, ожидается уход в сферу действия Кербина)
"MANEUVER" - впереди на орбите установлен манёвр
Примеры использования типа ORBIT:
print ship:orbit:LAN. // напечатает долготу восходящего узла орбиты активного крафта
print Jool:orbit:argumentofperiapsis. // напечатает аргумент перицентра орбиты Джула
print ship:orbit:LAN - target:orbit:LAN. // напечатает разность долготы восходящего узла активного крафта и установленной цели
Последний шаг, необходимый для полного знания об орбите, помимо орбитальных элементов - это узнать направление оси X, от которой отсчитывается долгота восходящего узла (направление полярной оси уже известно - оно имеет вид V(0,1,0) ). Это направление доступно из kOS как SOLARPRIMEVECTOR:
print SolarPrimeVector. // напечатает направление оси отсчёта небесной долготы в виде V(a,b,c)
В качестве упражнения, напишем несколько полезных функций для расчёта орбитальных направлений.
1. Вектор нормали к орбите. Определяется направлением момента импульса [r×v].
function OrbitNormVec {
parameter object is ship.
local objvec to object:orbit:position - object:body:position.
local objvel to object:velocity:orbit.
return vcrs(objvel, objvec):normalized. // порядок векторного произведения изменён, т.к. в игре левосторонняя система координат
}2. Направление линии узлов. Поскольку линия узлов лежит как в экваториальной плоскости, так и в плоскости орбиты, она перпендикулярна полярной оси планеты (V(0,1,0)) и нормали к орбите, т.е. направлена вдоль векторного произведения этих векторов. Направление на восходящий узел соответствует произведению [North×n] (см. рис. 4).
function DirAN {
parameter object is ship.
local orbn to OrbitNormVec(object).
return vcrs(orbn, V(0,1,0)):normalized.
}3. Линия узлов одной орбиты относительно другой. Считается аналогично экваториальной линии узлов, только вместо оси, направленной на север, необходимо взять нормаль к орбите, принятой за базовую.
function DirRelAN {
parameter baseobject, object is ship.
local orbn to OrbitNormVec(object).
local baseorbn to OrbitNormVec(baseobject).
return vcrs(orbn, baseorbn):normalized.
}4. Взаимное наклонение двух орбит.
Очевидно, равно углу между нормалями к орбитам:
function RelIncl {
parameter obj1, obj2 is ship.
local orbn1 to OrbitNormVec(obj1).
local orbn2 to OrbitNormVec(obj2).
return vang(orbn1,orbn2).
}5. Линия апсид. Она сонаправлена с вектором эксцентриситета.
function EccVec {
parameter object is ship.
local r to object:orbit:position - object:body:position.
local v to object:orbit:velocity.
local mu to object:body:mu.
return ( (vdot(v,v) - mu / r:mag) * r - vdot(r, v) * v ) / mu.
}6. Нормаль и линия узлов орбиты по заданным величинам долготы восходящего узла и наклонения.
Смотрим рисунок 4. Линия узлов получается поворотом оси X вокруг оси Z на долготу восходящего узла, нормаль получается поворотом оси Z вокруг линии узлов на наклонение. Воспользуемся функцией ANGLEAXIS для направлений, чтобы выполнить эти повороты. А поскольку линия узлов и нормаль всегда перпендикулярны, их удобно хранить в одной переменной направления, например, линию узлов в поле FOREVECTOR, нормаль в поле UPVECTOR.
function DirANNorm {
parameter lan, incl.
local basedir to lookdirup(SolarPrimeVector, V(0,1,0)).
set basedir to angleaxis(-lan, V(0,1,0))*basedir. // углы со знаком минус, т.к. в игре положительное направление вращения по часовой стрелке
set basedir to angleaxis(-incl, basedir:forevector)*basedir.
return basedir.
}
При необходимости, можно получить и линию апсид, повернув линию узлов вокруг нормали на аргумент перицентра.
Теперь используем эти функции для поворота круговой орбиты другую плоскость, задаваемую долготой восходящего узла и наклонением.
Начальную орбиту будем считать круговой, поворот будет производиться в один прожиг, причём так, чтобы конечная орбита также была круговой. Для простоты расчёта, манёвр ставится в восходящем узле, а не в ближайшем по времени.
Вектор скорости при манёвре следует повернуть на угол i по часовой стрелке вокруг радиус-вектора в восходящем узле (см. рис. 5). Манёвр имеет компоненты в направлении нормали к орбите и вектора орбитальной скорости.

Рисунок 5. Схема поворота орбитальной скорости в восходящем узле при изменении плоскости орбиты. NRM и PRG - оси нормали и орбитальной скорости на старой орбите.
Если рассматривать всё в осях (Radial, Normal, Prograde) относительно исходной орбитальной скорости, то исходный вектор орбитальной скорости имеет координаты (0, 0, V0), новый - (0, -V0sin i, V0cos i). Следовательно, вектор ΔV имеет компоненты (0, -V0sin i, V0(cos i - 1) ).
Замечание. При большом взаимном наклонении орбит может быть выгоднее делать поворот "через бесконечность", т.е. сначала поднять апоцентр к границе сферы действия, сменить наклонение в апоцентре, затем в перицентре опять опустить апоцентр. Здесь приводится простой скрипт, который эффективность манёвра не анализирует.
function ChangeLANInc {
parameter newlan, newincl.
local nv to OrbitNormVec(ship). // вектор нормали к орбите
local newnv to DirANNorm(newlan, newincl):upvector. // вектор нормали к новой орбите
local RelAN to vcrs( nv, newnv ). // направление на восходящий узел относительно новой орбиты
local rv to ship:orbit:position - body:position. // радиус-вектор из центра притяжения
// надо вычислить угол, который кораблю нужно пройти до восходящего узла
// vang() не подойдёт, т.к. не учитывает направление вращения
// для правильного учёта квадранта используем arctan2( sin, cos)
// синус угла с учётом знака - это проекция векторного произведения [RelAN, rv] на нормаль к орбите
// косинус угла - скалярное произведение (RelAN, rv)
local sinevec to vcrs(RelAN, rv).
local AngToAN to arctan2( vdot(nv, sinevec), vdot(RelAN, rv) ).
if AngToAN < 0 { set AngToAN to 360 + AngToAN. }
local TimeToAN to AngToAN/360 * ship:orbit:period. // верно только для круговой орбиты
local RelIncl to vang(nv, newnv).
local dvprg to velocity:orbit:mag * (cos(RelIncl) - 1).
local dvnrm to - velocity:orbit:mag * sin(RelIncl).
local nd to node(time:seconds + TimeToAN, 0, dvnrm, dvprg).
add nd.
}Более сложный пример - переход на более высокую круговую орбиту в другой плоскости. В этом случае выгодно сначала в одном из узлов поднять апоцентр без изменения плоскости (в итоге получится орбита с аргументом перицентра 0° или 180°), затем в апоцентре сделать комбинацию скругления орбиты и поворота в новую плоскость.
Манёвр подъёма апоцентра предлагаю рассчитать самостоятельно, приведу здесь только функцию комбинированного манёвра скругления и поворота орбиты в апоцентре.

Рисунок 6. Схема изменения орбитальной скорости в восходящем узле при комбинировании изменения плоскости орбиты и подъёма орбиты.
Будем считать, что первый манёвр произведён в нисходящем узле, т.е. апоцентр попадает в восходящий узел (аргумент перицентра 180°). По схеме на рис. 6 видим:
V1,PRG = V1 cos i
V1,NRM = -V1 sin i
ΔV = (0, -V1sin i, V1cos i - V0 )
На основе этого пишем функцию:
function RotateCWAndCircAtAP {
parameter i.
local Ra to body:radius + apoapsis.
local a0 to orbit:semimajoraxis.
local CrcSpd to sqrt( body:mu / Ra ).
local Va to sqrt( body:mu * (2/Ra - 1/a0) ).
local dvprg to CrcSpd * cos(i) - Va.
local dvnrm to -CrcSpd * sin(i).
local nd to node(time:seconds + eta:apoapsis, 0, dvnrm, dvprg).
add nd.
}Естественно, если нужно перейти на более низкую орбиту в другой плоскости, то порядок действий должен быть обратным - сначала опускается перицентр с одновременным поворотом плоскости, затем орбита скругляется в перицентре.
На этом завершаю настоящую часть руководства. Далее будет рассмотрен вопрос взлёта с поверхности сразу в нужную плоскость.
Hello there!
Дорогой Гость, чат доступен только для зарегистрированных пользователей.
Последние комментарии

ОБНОВЛЕНИЕ! Параллельный импорт EVE Raymarched Volumetrics версия "Иду на грозу" (июль2024)
доброго времени суток там случайно новых версий за полгода не вышло?
Kastronomicon, маяк Кербина
При всём уважении, в статье нет матана. Есть только элементарная математика.

ShineFix - мод для починки всех отражений и флагов в игре
В новой версии исправлено - теперь ресток тоже полностью поддерживается)

ShineFix - мод для починки всех отражений и флагов в игре
Shaddy и Shabby это два разных мода, ссылки в посте ведут на репозитории авторов, что априори самое

ShineFix - мод для починки всех отражений и флагов в игре
Я добавил в подпись актуальную версию, она будет обновляться автоматически, как и ссылка на неё)

Все комментарии..
Полный список последних комментариев
Последние сообщения с форума

Все сообщения..
Полный список последних сообщений
Loading...
Нашли ошибку?
Вы можете сообщить об этом администрации.
Выделив текст нажмите Ctrl+Alt