Теория и практика межпланетных перелетов. Часть 1.
1. Элементарная теория. Плоская задача достижения планеты
Итак, для простоты и понимания принципов расчета траекторий полета к другим планетам, рассмотрим эту задачу в следующих допущениях:
1. Орбиты планет - круговые, с радиусом равным большой полуоси
2. Орбиты планет лежат в одной плоскости
Траектория перелета от одной планеты к другой - это орбита вокруг центрального тела планетарной системы: Солнца в Солнечной, Кербола - в Кербальской. Наиболее выгодной с точки зрения затрат топлива будет орбита, изображенная на рисунке
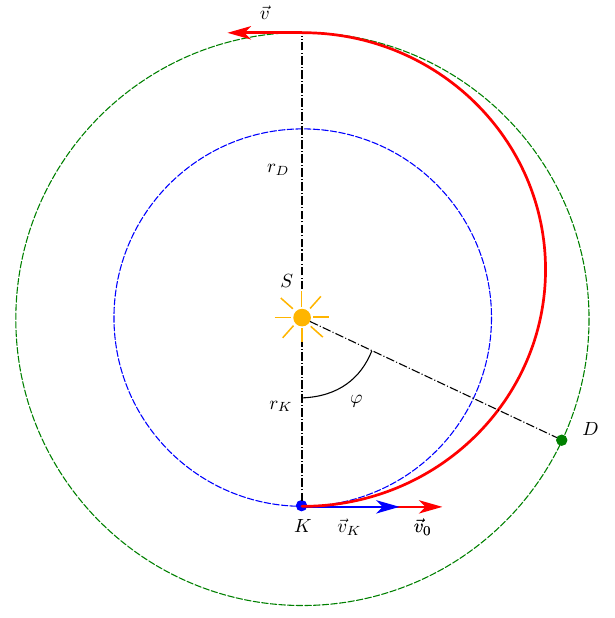
Такие траектории впервые были предложены Вальтером Гоманом в 1925 году, в его фундаментальном труде "Достижимость небесных тел".
Мы хотим долететь до Дюны, которая, по отношению к Кербину, является внешней планетой, то есть орбита Кербина пролегает целиком внутри орбиты Дюны. Для перелета к ней, нам следует двигаться вокруг Солнца-Кербола по эллипсу, который в двух точках будет касаться орбиты Кербина и орбиты Дюны. Встреча с Дюной произойдет в точке, строго противоположной точке старта.
Чтобы двигаться по такой орбите вокруг звезды на придется располагать в точке старта K скорость, достаточной для движения о изображенной траектории. Рассчитаем эту скорость. Нам на помощь придет закон сохранения полной механической энергии
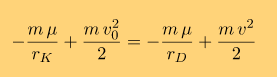
Слева - сумма потенциальной и кинетической энергии аппарата при отлете от Кербина, справа - та же сумма, но в момент прибытия в район Дюны. Масса m - масса космического аппарата, "мю" - гравитационный параметр центрального тела (звезды, Кербола!)
Мы не знаем скорость v, с которой прибудем к Дюне, но можем выразить её через начальную скорость у Кербина пользуясь вторым законом Кеплера

В конечном итоге мы получим формулу для скорости отлета к Дюне
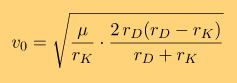
Учитываем, что
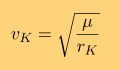
как раз скорость движения Кербина по орбите вокруг солнца (если считать его орбиту круговой), поэтому формулу скорости отлета можно упростить

Проведя расчет получим v0 = 9960,2 м/с. Многовато, не правда ли?
Правда вот тут мы не должны забывать - стартуем мы с Кербина, а все что находится на Кербине уже несется в пространстве вокруг солнца со скоростью движения Кербина по орбите, а это - не много, не мало 9063,7 м/с, которые у нас уже есть. И нам не хватает всего-то 896,5 м/с для полного счастья. Эту добавочную скорость мы получим, правильно стартуя с околокербинской орбиты.
Как известно, для того чтобы "убежать" от какого-либо небесного тела надо развить в его окрестности параболическую скорость. Если мы находимся прямо на поверхности этого тела, то такую скорость называют второй космической скоростью для данного тела. Если мы стартуем с орбиты Кербина имея параболическую скорость (а это - 3222,9 м/с на орбите высотой 80 км), то улетая от Кербина по параболе, мы будем медленно и верно терять скорость, и оказавшись очень далеко, за пределами сферы гравитационного действия Кербина, будем иметь, относительно него нулевую скорость. Такой аппарат будет двигаться по той же самой орбите, что движется планета, которую он покинул.
А вот если мы стартуем со скоростью более параболической, то улетать мы будем по гиперболе, и в пределе, оказавшись очень далеко от родной планеты, мы будем иметь относительно неё некоторую постоянную скорость, так называемую скорость "на бесконечности". Попробуем определить величину этой скорости, снова воспользовавшись законом сохранения энергии. Учтем, что очень далеко, за пределами гравитационного колодца планеты, потенциальная энергия тела в её гравитационном поле равна нулю. Тогда, энергобаланс таков

здесь h - высота низкой орбиты вокруг Кербина, с которой производится старт; R - радиус Кербина; "мю" с индексом "К" - гравитационный параметр Кербина; v с индексом "бесконечность" - скорость, которую мы будем иметь очень-очень-очень далеко от планеты. Из этой формулы получаем скорость старта, необходимую для получения заданной скорости "на бесконечности"

что дает скорость vM = 3345,3 м/с, которую мы должны иметь при старте с орбиты Кербина. Но не торопимся.
Механика игры, на сегодняшний день, такова, что для моделирования полета в ней используется метод склеивания конических сечений. Всё пространство в планетарной системе разбито на области - гравитационные сферы действия тел, внутри которых считается, что на космический корабль не влияет никакое другое тело, кроме того, внутри сферы действия которого оно находится. При выходе из сферы действия (например Кербина) скорость, с которой корабль вылетает складывается векторно с орбитальной скоростью покидаемого тела, и по модулю и направлению полученной скорости (при вылете с Кербина это будет скорость относительно Солнца) строится новая орбита, вокруг того тела, в сферу влияния которого мы влетаем. И наоборот - влетая в сферу действия, например сферу действия Мун относительно Кербина, из скорости входа вычитается скорость орбитального движения Мун, полученная скорость относительно Мун служит для построения последующей траектории.
Таким образом, мы можем считать, что покинули гравитационное поле Кербина, если удалились от него на расстояние равное 84159,3 километра - таков радиус сферы действия Кербина относительно Кербола. Более точно этот радиус определяется формулой

где mK - масса Кербина; mS - масса Кербола; aK - большая полуось орбиты Кербина (среднее расстояние до Кербола). Соответственно мы уточняем скорость старта с орбиты Кербина
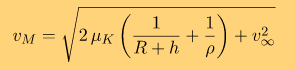
При расчете получаем скорость vM = 3332,9 м/с. С учетом того, что на круговой орбите высотой 80 км мы будем иметь орбитальную круговую скорость vk = 2278,9 м/с, мы получаем то приращение скорости, которое должен сообщить нашему "пепелацу" разгонный блок

Это и есть та "дельта", которую должен обеспечить нам разгонный блок для старта к Дюне. И, надо сказать, это значение весьма близко к тем цифрам, что мы имеем на практике при полете к Дюне.
Кроме того, разгон следует осуществлять в определенной точке орбиты. Понять в какой именно нам поможет чертеж

На рисунке видно, что старт следует производить в сторону орбитального движения Кербина, так, чтобы вектор скорости аппарата при выходе из сферы действия был параллелен вектору скорости Кербина. Положение точки старта M будем задавать как угол "пси" между точкой старта и направлением на Солнце. Поупражнявшись в геометрии и вспомнив свойства конических сечений, получаем значение этого угла

где e - эксцентриситет гиперболы, который зависит от начальной скорости в перицентре и круговой скорости на данной высоте над планетой

Нашем случае эксцентриситет гиперболы e = 1,1389. Угол psi = 118,6 градуса.
Таким образом, запуск двигателей разгонного блока для старта к Дюне всегда будет происходить над ночной стороной Кербина. Но это ещё не всё.
Выход из сферы действия Кербина должен произойти в такой момент времени, чтобы при прибытии корабля в противоположную точку траектории перелета там же оказалась и Дюна. Время движения по траектории перелета равно половине периода обращения корабля по орбите вокруг Солнца, на которую он выходит при перелете, что есть

где a - большая полуось орбиты перелета. Её легко посчитать
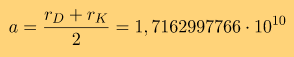
естественно, в метрах. Время перелета, выраженное в секундах, tau = 6682942 с. Если перевести это значение в Кербальский календарь (6 часов в сутках и 426 суток в году), то выходит 309 дней 2 часа 22 минуты 22 секунды. Теперь определим взаимное расположение Кербина и Дюны, для того, чтобы после выхода из сферы действия Кербина и перелета мы попали в Дюну. Период обращения Дюны по орбите, если считать эту орбиту круговой, равен Td = 17737240,6 секунд. Значит за одну секунду Дюна проходит дугу равную

градусов. За время перелета она должна пробежать по орбите дугу
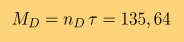
градуса. Соответственно, Дюна должна опережать Кербин на угол

Угол phi называют фазовым углом.
2. Суровая реальность...
Проведенный нами расчет очень приближенный. Орбиты - не окружности а эллипсы. Плоскости орбит не совпадают. Поэтому в реальности расчет траектории перелета к планете - сложная задача, сопряженная с решением так называемой задачи Ламберта. А ещё мы не учли время движения по гиперболе после старта с Кербина.
Однако, этот расчет показывает основные принципы планирования полета к внешней планете. На его основе нетрудно сориентироваться при планирование полета в игре.
На этом первую часть цикла гайдов по межпланетным полетам я закончу. В дальнейшем мы рассмотрим, как перевести полученные нами знания в практическую плоскость и рассмотрим:
1. Планирование траектории в KSP
2. Коррекцию траектории
3. Выход в заданный район посадки на планету
4. Посадку и взлет с планеты.
5. Обратный перелет
6. Подход к Кербину и торможение в атмосфере с гиперболической скоростью
Продолжение следует...
Итак, для простоты и понимания принципов расчета траекторий полета к другим планетам, рассмотрим эту задачу в следующих допущениях:
1. Орбиты планет - круговые, с радиусом равным большой полуоси
2. Орбиты планет лежат в одной плоскости
Траектория перелета от одной планеты к другой - это орбита вокруг центрального тела планетарной системы: Солнца в Солнечной, Кербола - в Кербальской. Наиболее выгодной с точки зрения затрат топлива будет орбита, изображенная на рисунке

Такие траектории впервые были предложены Вальтером Гоманом в 1925 году, в его фундаментальном труде "Достижимость небесных тел".
Мы хотим долететь до Дюны, которая, по отношению к Кербину, является внешней планетой, то есть орбита Кербина пролегает целиком внутри орбиты Дюны. Для перелета к ней, нам следует двигаться вокруг Солнца-Кербола по эллипсу, который в двух точках будет касаться орбиты Кербина и орбиты Дюны. Встреча с Дюной произойдет в точке, строго противоположной точке старта.
Чтобы двигаться по такой орбите вокруг звезды на придется располагать в точке старта K скорость, достаточной для движения о изображенной траектории. Рассчитаем эту скорость. Нам на помощь придет закон сохранения полной механической энергии
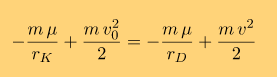
Слева - сумма потенциальной и кинетической энергии аппарата при отлете от Кербина, справа - та же сумма, но в момент прибытия в район Дюны. Масса m - масса космического аппарата, "мю" - гравитационный параметр центрального тела (звезды, Кербола!)
Мы не знаем скорость v, с которой прибудем к Дюне, но можем выразить её через начальную скорость у Кербина пользуясь вторым законом Кеплера

В конечном итоге мы получим формулу для скорости отлета к Дюне
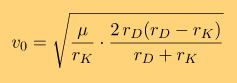
Учитываем, что
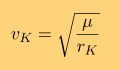
как раз скорость движения Кербина по орбите вокруг солнца (если считать его орбиту круговой), поэтому формулу скорости отлета можно упростить

Проведя расчет получим v0 = 9960,2 м/с. Многовато, не правда ли?
Правда вот тут мы не должны забывать - стартуем мы с Кербина, а все что находится на Кербине уже несется в пространстве вокруг солнца со скоростью движения Кербина по орбите, а это - не много, не мало 9063,7 м/с, которые у нас уже есть. И нам не хватает всего-то 896,5 м/с для полного счастья. Эту добавочную скорость мы получим, правильно стартуя с околокербинской орбиты.
Как известно, для того чтобы "убежать" от какого-либо небесного тела надо развить в его окрестности параболическую скорость. Если мы находимся прямо на поверхности этого тела, то такую скорость называют второй космической скоростью для данного тела. Если мы стартуем с орбиты Кербина имея параболическую скорость (а это - 3222,9 м/с на орбите высотой 80 км), то улетая от Кербина по параболе, мы будем медленно и верно терять скорость, и оказавшись очень далеко, за пределами сферы гравитационного действия Кербина, будем иметь, относительно него нулевую скорость. Такой аппарат будет двигаться по той же самой орбите, что движется планета, которую он покинул.
А вот если мы стартуем со скоростью более параболической, то улетать мы будем по гиперболе, и в пределе, оказавшись очень далеко от родной планеты, мы будем иметь относительно неё некоторую постоянную скорость, так называемую скорость "на бесконечности". Попробуем определить величину этой скорости, снова воспользовавшись законом сохранения энергии. Учтем, что очень далеко, за пределами гравитационного колодца планеты, потенциальная энергия тела в её гравитационном поле равна нулю. Тогда, энергобаланс таков

здесь h - высота низкой орбиты вокруг Кербина, с которой производится старт; R - радиус Кербина; "мю" с индексом "К" - гравитационный параметр Кербина; v с индексом "бесконечность" - скорость, которую мы будем иметь очень-очень-очень далеко от планеты. Из этой формулы получаем скорость старта, необходимую для получения заданной скорости "на бесконечности"

что дает скорость vM = 3345,3 м/с, которую мы должны иметь при старте с орбиты Кербина. Но не торопимся.
Механика игры, на сегодняшний день, такова, что для моделирования полета в ней используется метод склеивания конических сечений. Всё пространство в планетарной системе разбито на области - гравитационные сферы действия тел, внутри которых считается, что на космический корабль не влияет никакое другое тело, кроме того, внутри сферы действия которого оно находится. При выходе из сферы действия (например Кербина) скорость, с которой корабль вылетает складывается векторно с орбитальной скоростью покидаемого тела, и по модулю и направлению полученной скорости (при вылете с Кербина это будет скорость относительно Солнца) строится новая орбита, вокруг того тела, в сферу влияния которого мы влетаем. И наоборот - влетая в сферу действия, например сферу действия Мун относительно Кербина, из скорости входа вычитается скорость орбитального движения Мун, полученная скорость относительно Мун служит для построения последующей траектории.
Таким образом, мы можем считать, что покинули гравитационное поле Кербина, если удалились от него на расстояние равное 84159,3 километра - таков радиус сферы действия Кербина относительно Кербола. Более точно этот радиус определяется формулой

где mK - масса Кербина; mS - масса Кербола; aK - большая полуось орбиты Кербина (среднее расстояние до Кербола). Соответственно мы уточняем скорость старта с орбиты Кербина
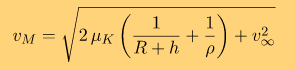
При расчете получаем скорость vM = 3332,9 м/с. С учетом того, что на круговой орбите высотой 80 км мы будем иметь орбитальную круговую скорость vk = 2278,9 м/с, мы получаем то приращение скорости, которое должен сообщить нашему "пепелацу" разгонный блок

Это и есть та "дельта", которую должен обеспечить нам разгонный блок для старта к Дюне. И, надо сказать, это значение весьма близко к тем цифрам, что мы имеем на практике при полете к Дюне.
Кроме того, разгон следует осуществлять в определенной точке орбиты. Понять в какой именно нам поможет чертеж

На рисунке видно, что старт следует производить в сторону орбитального движения Кербина, так, чтобы вектор скорости аппарата при выходе из сферы действия был параллелен вектору скорости Кербина. Положение точки старта M будем задавать как угол "пси" между точкой старта и направлением на Солнце. Поупражнявшись в геометрии и вспомнив свойства конических сечений, получаем значение этого угла

где e - эксцентриситет гиперболы, который зависит от начальной скорости в перицентре и круговой скорости на данной высоте над планетой

Нашем случае эксцентриситет гиперболы e = 1,1389. Угол psi = 118,6 градуса.
Таким образом, запуск двигателей разгонного блока для старта к Дюне всегда будет происходить над ночной стороной Кербина. Но это ещё не всё.
Выход из сферы действия Кербина должен произойти в такой момент времени, чтобы при прибытии корабля в противоположную точку траектории перелета там же оказалась и Дюна. Время движения по траектории перелета равно половине периода обращения корабля по орбите вокруг Солнца, на которую он выходит при перелете, что есть

где a - большая полуось орбиты перелета. Её легко посчитать
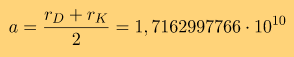
естественно, в метрах. Время перелета, выраженное в секундах, tau = 6682942 с. Если перевести это значение в Кербальский календарь (6 часов в сутках и 426 суток в году), то выходит 309 дней 2 часа 22 минуты 22 секунды. Теперь определим взаимное расположение Кербина и Дюны, для того, чтобы после выхода из сферы действия Кербина и перелета мы попали в Дюну. Период обращения Дюны по орбите, если считать эту орбиту круговой, равен Td = 17737240,6 секунд. Значит за одну секунду Дюна проходит дугу равную

градусов. За время перелета она должна пробежать по орбите дугу
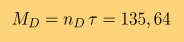
градуса. Соответственно, Дюна должна опережать Кербин на угол

Угол phi называют фазовым углом.
2. Суровая реальность...
Проведенный нами расчет очень приближенный. Орбиты - не окружности а эллипсы. Плоскости орбит не совпадают. Поэтому в реальности расчет траектории перелета к планете - сложная задача, сопряженная с решением так называемой задачи Ламберта. А ещё мы не учли время движения по гиперболе после старта с Кербина.
Однако, этот расчет показывает основные принципы планирования полета к внешней планете. На его основе нетрудно сориентироваться при планирование полета в игре.
На этом первую часть цикла гайдов по межпланетным полетам я закончу. В дальнейшем мы рассмотрим, как перевести полученные нами знания в практическую плоскость и рассмотрим:
1. Планирование траектории в KSP
2. Коррекцию траектории
3. Выход в заданный район посадки на планету
4. Посадку и взлет с планеты.
5. Обратный перелет
6. Подход к Кербину и торможение в атмосфере с гиперболической скоростью
Продолжение следует...
Новость отредактировал: Басила - 21 мая 2022 в 22:05
Hello there!
Дорогой Гость, чат доступен только для зарегистрированных пользователей.
Последние комментарии
ОБНОВЛЕНИЕ! Параллельный импорт EVE Raymarched Volumetrics версия "Иду на грозу" (июль2024)
Как сделать облака и на других планетах по типу Евы или джула. И как сделать так чтобы на дюне были
Kerbal Space Program (KSP) 1.12.5 скачать - "On Final Approach" + DLC
тут хотя бы не троян?
[РУСИФИКАТОР] KSP 1.0.x
Спасибо огромное на финальной версий 1.12.5 всё переведено идеально
Параллельный импорт EVE Raymarched Volumetrics - RSS "Облака планеты Земля"
я видеокарта gtx660 мод потянет?

ОБНОВЛЕНИЕ! Параллельный импорт EVE Raymarched Volumetrics версия "Иду на грозу" (июль2024)
доброго времени суток там случайно новых версий за полгода не вышло?

Все комментарии..
Полный список последних комментариев
Последние сообщения с форума

Все сообщения..
Полный список последних сообщений
Loading...
Нашли ошибку?
Вы можете сообщить об этом администрации.
Выделив текст нажмите Ctrl+Alt