Теория и практика межпланетных перелетов. Часть 2.
1. Кеплеровы элементы планетарной орбиты
В самом-самом общем случае орбита планеты выглядит так
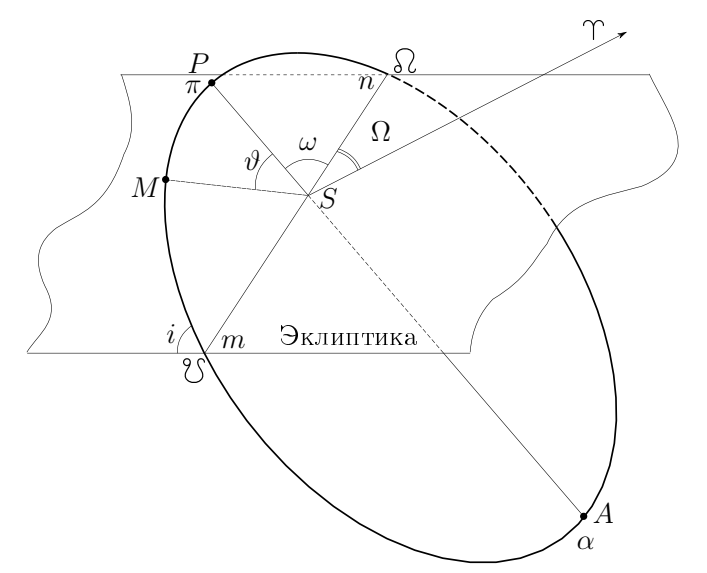
Для того чтобы знать, как планета расположена в пространстве необходимо, во-первых, задать точку отсчета. В Солнечной системе в качестве опорной плоскости, по отношению к которой рассматривают орбиты планет берут плоскость орбиты Земли, называя её плоскостью эклиптики, или просто эклиптикой. К гадалке не ходи (да и если внимательно почитать вики, становится ясно), что эклиптикой в Кербальской системе является плоскость орбиты Кербина.
В качестве направления отсчета углов в Солнечной системе выбирается прямая, проходящая через центр Солнца в сторону точки, расположенной в созвездии Овна и называемой точкой весеннего равноденствия. Называется она так потому, что на земном небе, положение Солнца и положения этой точки совпадают именно 23 марта, вдень весеннего равноденствия.
В Кербальской системе так же принято направление отсчета углов, однако связать его с какой-либо точкой на небе не выйдет - в KSP нет нормального звездного неба - звезды нарисованы и ни одна из них, кроме Кербола не может быть идентифицирована. Но нас это не волнует - таковое направление имеется, а нас будут больше интересовать относительные показатели положения планет, чем абсолютные. Будем считать, что в KSP так же имеется точка весеннего равноденсвия (ТВР), на чертеже выше обозначенное значком Овна.
Итак, как же задать положение планеты? В плоскости своей орбиты её положение задается одним единственным углом theta - истинной аномалией - угол между текущим положением планеты и направлением на перицентр (между отрезками SM и SP). Плоскость орбиты может быть наклонена к плоскости эклиптики (плоскость орбиты Кербина!) под некоторым углом i, который называется наклонением орбиты. В этом случае она пересекат эклиптику по прямой nm. В точке n находится, так называемый, восходящий узел орбиты - точка лежащая в эклиптике, двигаясь из которой планета начинает подниматься над плоскостью эклиптики. Угол между между прямымой Sn и направлением на ТВР называется долготой восходящего узла Omega. И, наконец, положение перицентра по отношению к восходящему узлу задаемся углом nSP, на рисунке обозначенном omega - этот угол называют аргумент перицентра.
Так, ну а как же быть с расстоянием от планеты до солнца и как связать все это с временем? Для этого рассмотрим подробнее параметры эллиптической орбиты

Согласно первому закону Кеплера - орбита планеты - эллипс, в одном из фокусов которого находится солнце. На рисунке солнце находится в точке S. Геометрический же центр эллипса находится в точке C. Длины отрезков AC = CP = a - большая полуось орбиты, среднее арифметическое между наибольшим и наименьшим расстояниями от планеты до солнца
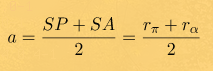
Мерой "сплюснутости" эллипса служит эксцентриситет, выражающий, насколько далеко фокус эллипса отстоит от его геометрического центра
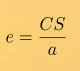
Если e = 0, то орбита планеты будет круговой, с радиусом равным a. Круговую орбиту имеет например Кербин - расстояние от него до Кербола не меняется, что сильно облегчает жизнь при расчетах. В реальной жизни идеальных круговых орбит не наблюдается, у той же Земли, эксцентриситет, хоть и небольшой, но все же не ноль. Для эллиптических орбит значение эксцентриситета лежит в пределах 0 < e < 1.
Большая полуось и эксцентриситет полностью задают форму орбиты, и, зная истинную аномалию можно вычислить расстояние от планеты до солнца
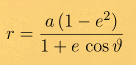
Зная большую полуось можно рассчитать время полного оборота планеты по орбите - сидерический период обращения или просто период обращения
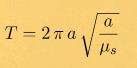
И вот тут возникает резонный вывод - для того чтобы осуществить перелет от одной планеты к другой, надо веть знать их взаимное расположение в любой интересующий нас момент времени. Иначе как мы определим, в какой год, день и час между планетами будет нужный для перелета фазовый угол.
2. Общий метод вычисления эфемерид
Чтобы связать положение планеты на орбите со временем нам надо знать в каком году, в какой день, час, минуту, и даже секунду, планеты последний раз находилась в перицентре. Желательно, чтобы эта информация была как можно более свежей. В тех астрономических таблицах с которыми я столкнулся впервые как раз и была указана дата прохождения планетой перигелия tp.
В KSP этот момент задается другим параметром - средней аномалией. Средняя аномалия - угол M, который прошла бы планета по орбите за время t, если бы двигалась равномерно с угловой скоростью
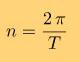
где T - период обращения планеты. В KSP-вики для каждой планеты указана средняя аномалия M0 для эпохи J0, то есть в для даты 1y 1d 0h 0m 0s (в первый год, первый день 0 часов 0 минут 0 секунд по кербальскому времени). Значит можно вычислить среднюю аномалию для любого другого момента времени t
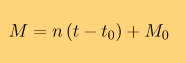
где t0 - момент времени, в секундах, для той эпохи, которой соответствует значение M0. Для кербальской системы t0 = 0. Интересующий нас момент времени t в секундах можно рассчитать по дате кербальского календаря, пользуясь формулой
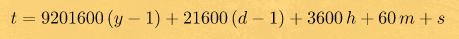
где y - год; d - день; h - час; m - минуты; s - секунды.
Для Кербина этим можно и ограничится - раз его орбита круговая, то истинная аномалия равна средней. Если орбита эллиптическая, то для нахождения истинной аномалии придется решить уравнение Кеплера

где E - угол, именуемый эксцентрической аномалией. Это уравнение получено Кеплером на основе геометрических представлений и вытекает из его законов движения планет. Оно получено задолго до появления законов Ньютона, применяя которые к движению планеты можно крайне строго вывести это самое уравнение. Оно - результат решения дифференциального уравнения движения планеты, и чтобы получить эту формулу, приходится брать интеграл с хитринкой.
Но нам это без надобности, нам надо решить это трансцендентное уравнение, чтобы найти угол E, зная который мы получим истинную аномалию
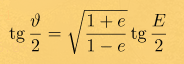
и расстояние от планеты до солнца
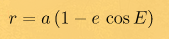
А теперь опробуем данные формулы для вычисление положения скажем... да той же Дюны, для интересующего нас момента времени
3. Успехи кербальской астрономии
Для планеты Дюна, согласно KSP-вики имеем
Большая полуось орбиты a = 20726155264 м
Эксцентриситет e = 0.05
Наклонение орбиты i = 0.06 градуса
Аргумент перицентра omega = 0
Долгота восходящего узла Omega = 135.5 градуса
Средняя аномалия M0 = 3.14 радиан
Период обращения T = 17315400 c
На моем календаре в KSP 31 год 346 день 5 часов 32 минуты. В секундах это будет

Вычисляем истинную аномалию
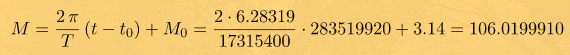
Замечу ещё раз - вычисленный угол задан в радианах. Раз он больше двух пи, то за 31 год Дюна совершила не один оборот вокруг Кербола. Отбросив лишние обороты получим
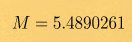
Теперь самое вкусное - находим эксцентрическую аномалию, решая уравнение Кеплера. Проще всего (но дольше всего) его решить используя метод итераций или метод последовательных приближений, описываемый рекурентной формулой
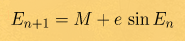
В качестве начального приближения возьмем среднюю аномалию
Теперь вычислим новое, первое, приближение
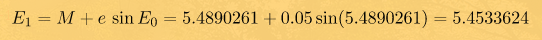
Ага, мы видим, что полученное значение отличается от предыдущего. Принимая его вместо E вычисляем следующие приближение, до тех пор, пока разница между текущим приближением и вновь вычисленным не станет меньше некоторой нужной нам точности. Скажем, пусть совпадут шесть знаков после запятой
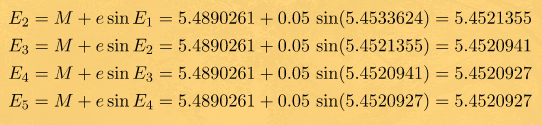
Вуаля! На пятой итерации получилось совпадение в даже в седьмом знаке. Принимаем последнее значение в качестве эксцентрической аномалии E = 5.4520927 рад. Теперь, наконец, вычисляем истинную аномалию

Вычисляя арктангенс и учитывая, что эксцентрическая аномалия - развернутый угол, получаем значение истинной аномалии
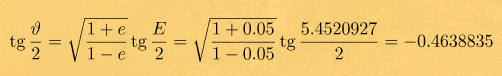
Это примерно 310.23 градуса - в рассматриваемый момент времени Дюна не добегает около 49 градусов до перицентра.
Грош цена бы этим вычислениям, если они не совпадают с тем, что мы должны увидеть в игре. Проверим?
4. Эксперимент в KSP
Лезем в KSP и, с помощью плагина HyperEdit переводим дату на UT 31y 346d 5h 32m. Отставить гнилые помидоры и тухлые яйца! Да-да, я читал что HyperEdit это чит... А что плохого в том, чтобы перевести дату на нужную, вместо того чтобы судорожно ловить стартовое окно 100000х варпом? Наша задача - понять механику игры, и тут грех не использовать удобное средство. В окне HyperEdit дата вводится в секундах от эпохи J0.
Вот положение Дюны

Она явно не в крайней точке орбиты - высота над Керболом меняется на глазах.
Дальше, путем вычислений, обратных проведенным выше, находим, что Дюна была в перицентра в момент UT 1y 402d 0h 8m 9s. Ставим эту дату

Это явный перицентр - расстояние до звезды на глаз не меняется, а значит в этой точке крайне мала радиальная скорость. Теперь совмещаем два скрина и меряем угол

С учетом того, что мышкой не вывести плоскость точно и учитывая погрешность измерения угла в Inkscape делаем вывод, что мы всё верно расчитали.
Наконец вычислим расстояние от Дюны до Кербола в UT 31y 346d 5h 32m. И вот тут выходит некоторая неточность, ибо с учетом радиуса Кербола в 261600000 м мы получаем высоту над Керболом 19766012240 м, а на скриншоте немного другое число. Что ж, попробую выяснить в чём дело, а пока
Выводы
Аналогичная процедура применима к любой другой планете кербальской системы, и к любой планете Солнечной системы. Теперь мы умеем вычислять положение планет в KSP.
В следующий раз мы увидим, для чего нужны параметры ориентации плоскости орбиты в пространстве, о которых мы говорили. Наша задача научится вычислять эклиптическую долготу планеты, веть разность эклиптических долгот планеты и Кербина и есть тот самый фазовый угол, необходимый для точного расчета окна старта.
Продолжение следует...
P.S.: Небольшое исследование внутренностей KSP (законными методами, через SDK) дало понять причину неточного расчета. Дело в том что в вики даются округленные параметры орбит. Текст не переписываю, приложу только результат того же расчета но с реальными параметрами орбит
В самом-самом общем случае орбита планеты выглядит так

Для того чтобы знать, как планета расположена в пространстве необходимо, во-первых, задать точку отсчета. В Солнечной системе в качестве опорной плоскости, по отношению к которой рассматривают орбиты планет берут плоскость орбиты Земли, называя её плоскостью эклиптики, или просто эклиптикой. К гадалке не ходи (да и если внимательно почитать вики, становится ясно), что эклиптикой в Кербальской системе является плоскость орбиты Кербина.
В качестве направления отсчета углов в Солнечной системе выбирается прямая, проходящая через центр Солнца в сторону точки, расположенной в созвездии Овна и называемой точкой весеннего равноденствия. Называется она так потому, что на земном небе, положение Солнца и положения этой точки совпадают именно 23 марта, вдень весеннего равноденствия.
В Кербальской системе так же принято направление отсчета углов, однако связать его с какой-либо точкой на небе не выйдет - в KSP нет нормального звездного неба - звезды нарисованы и ни одна из них, кроме Кербола не может быть идентифицирована. Но нас это не волнует - таковое направление имеется, а нас будут больше интересовать относительные показатели положения планет, чем абсолютные. Будем считать, что в KSP так же имеется точка весеннего равноденсвия (ТВР), на чертеже выше обозначенное значком Овна.
Итак, как же задать положение планеты? В плоскости своей орбиты её положение задается одним единственным углом theta - истинной аномалией - угол между текущим положением планеты и направлением на перицентр (между отрезками SM и SP). Плоскость орбиты может быть наклонена к плоскости эклиптики (плоскость орбиты Кербина!) под некоторым углом i, который называется наклонением орбиты. В этом случае она пересекат эклиптику по прямой nm. В точке n находится, так называемый, восходящий узел орбиты - точка лежащая в эклиптике, двигаясь из которой планета начинает подниматься над плоскостью эклиптики. Угол между между прямымой Sn и направлением на ТВР называется долготой восходящего узла Omega. И, наконец, положение перицентра по отношению к восходящему узлу задаемся углом nSP, на рисунке обозначенном omega - этот угол называют аргумент перицентра.
Так, ну а как же быть с расстоянием от планеты до солнца и как связать все это с временем? Для этого рассмотрим подробнее параметры эллиптической орбиты

Согласно первому закону Кеплера - орбита планеты - эллипс, в одном из фокусов которого находится солнце. На рисунке солнце находится в точке S. Геометрический же центр эллипса находится в точке C. Длины отрезков AC = CP = a - большая полуось орбиты, среднее арифметическое между наибольшим и наименьшим расстояниями от планеты до солнца
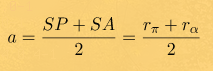
Мерой "сплюснутости" эллипса служит эксцентриситет, выражающий, насколько далеко фокус эллипса отстоит от его геометрического центра
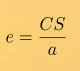
Если e = 0, то орбита планеты будет круговой, с радиусом равным a. Круговую орбиту имеет например Кербин - расстояние от него до Кербола не меняется, что сильно облегчает жизнь при расчетах. В реальной жизни идеальных круговых орбит не наблюдается, у той же Земли, эксцентриситет, хоть и небольшой, но все же не ноль. Для эллиптических орбит значение эксцентриситета лежит в пределах 0 < e < 1.
Большая полуось и эксцентриситет полностью задают форму орбиты, и, зная истинную аномалию можно вычислить расстояние от планеты до солнца
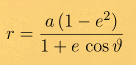
Зная большую полуось можно рассчитать время полного оборота планеты по орбите - сидерический период обращения или просто период обращения
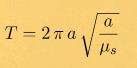
И вот тут возникает резонный вывод - для того чтобы осуществить перелет от одной планеты к другой, надо веть знать их взаимное расположение в любой интересующий нас момент времени. Иначе как мы определим, в какой год, день и час между планетами будет нужный для перелета фазовый угол.
2. Общий метод вычисления эфемерид
Чтобы связать положение планеты на орбите со временем нам надо знать в каком году, в какой день, час, минуту, и даже секунду, планеты последний раз находилась в перицентре. Желательно, чтобы эта информация была как можно более свежей. В тех астрономических таблицах с которыми я столкнулся впервые как раз и была указана дата прохождения планетой перигелия tp.
В KSP этот момент задается другим параметром - средней аномалией. Средняя аномалия - угол M, который прошла бы планета по орбите за время t, если бы двигалась равномерно с угловой скоростью
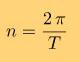
где T - период обращения планеты. В KSP-вики для каждой планеты указана средняя аномалия M0 для эпохи J0, то есть в для даты 1y 1d 0h 0m 0s (в первый год, первый день 0 часов 0 минут 0 секунд по кербальскому времени). Значит можно вычислить среднюю аномалию для любого другого момента времени t
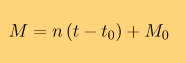
где t0 - момент времени, в секундах, для той эпохи, которой соответствует значение M0. Для кербальской системы t0 = 0. Интересующий нас момент времени t в секундах можно рассчитать по дате кербальского календаря, пользуясь формулой
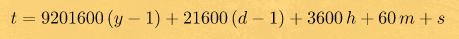
где y - год; d - день; h - час; m - минуты; s - секунды.
Для Кербина этим можно и ограничится - раз его орбита круговая, то истинная аномалия равна средней. Если орбита эллиптическая, то для нахождения истинной аномалии придется решить уравнение Кеплера

где E - угол, именуемый эксцентрической аномалией. Это уравнение получено Кеплером на основе геометрических представлений и вытекает из его законов движения планет. Оно получено задолго до появления законов Ньютона, применяя которые к движению планеты можно крайне строго вывести это самое уравнение. Оно - результат решения дифференциального уравнения движения планеты, и чтобы получить эту формулу, приходится брать интеграл с хитринкой.
Но нам это без надобности, нам надо решить это трансцендентное уравнение, чтобы найти угол E, зная который мы получим истинную аномалию
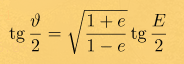
и расстояние от планеты до солнца
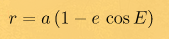
А теперь опробуем данные формулы для вычисление положения скажем... да той же Дюны, для интересующего нас момента времени
3. Успехи кербальской астрономии
Для планеты Дюна, согласно KSP-вики имеем
Большая полуось орбиты a = 20726155264 м
Эксцентриситет e = 0.05
Наклонение орбиты i = 0.06 градуса
Аргумент перицентра omega = 0
Долгота восходящего узла Omega = 135.5 градуса
Средняя аномалия M0 = 3.14 радиан
Период обращения T = 17315400 c
На моем календаре в KSP 31 год 346 день 5 часов 32 минуты. В секундах это будет

Вычисляем истинную аномалию
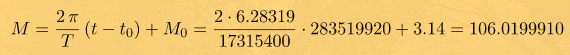
Замечу ещё раз - вычисленный угол задан в радианах. Раз он больше двух пи, то за 31 год Дюна совершила не один оборот вокруг Кербола. Отбросив лишние обороты получим
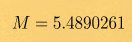
Теперь самое вкусное - находим эксцентрическую аномалию, решая уравнение Кеплера. Проще всего (но дольше всего) его решить используя метод итераций или метод последовательных приближений, описываемый рекурентной формулой
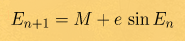
В качестве начального приближения возьмем среднюю аномалию
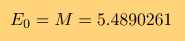
Теперь вычислим новое, первое, приближение
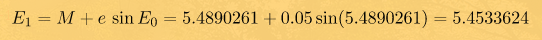
Ага, мы видим, что полученное значение отличается от предыдущего. Принимая его вместо E вычисляем следующие приближение, до тех пор, пока разница между текущим приближением и вновь вычисленным не станет меньше некоторой нужной нам точности. Скажем, пусть совпадут шесть знаков после запятой
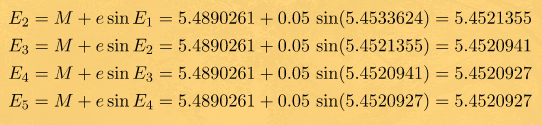
Вуаля! На пятой итерации получилось совпадение в даже в седьмом знаке. Принимаем последнее значение в качестве эксцентрической аномалии E = 5.4520927 рад. Теперь, наконец, вычисляем истинную аномалию

Вычисляя арктангенс и учитывая, что эксцентрическая аномалия - развернутый угол, получаем значение истинной аномалии
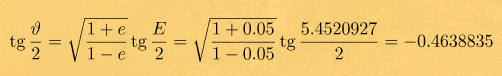
Это примерно 310.23 градуса - в рассматриваемый момент времени Дюна не добегает около 49 градусов до перицентра.
Грош цена бы этим вычислениям, если они не совпадают с тем, что мы должны увидеть в игре. Проверим?
4. Эксперимент в KSP
Лезем в KSP и, с помощью плагина HyperEdit переводим дату на UT 31y 346d 5h 32m. Отставить гнилые помидоры и тухлые яйца! Да-да, я читал что HyperEdit это чит... А что плохого в том, чтобы перевести дату на нужную, вместо того чтобы судорожно ловить стартовое окно 100000х варпом? Наша задача - понять механику игры, и тут грех не использовать удобное средство. В окне HyperEdit дата вводится в секундах от эпохи J0.
Вот положение Дюны

Она явно не в крайней точке орбиты - высота над Керболом меняется на глазах.
Дальше, путем вычислений, обратных проведенным выше, находим, что Дюна была в перицентра в момент UT 1y 402d 0h 8m 9s. Ставим эту дату

Это явный перицентр - расстояние до звезды на глаз не меняется, а значит в этой точке крайне мала радиальная скорость. Теперь совмещаем два скрина и меряем угол

С учетом того, что мышкой не вывести плоскость точно и учитывая погрешность измерения угла в Inkscape делаем вывод, что мы всё верно расчитали.
Наконец вычислим расстояние от Дюны до Кербола в UT 31y 346d 5h 32m. И вот тут выходит некоторая неточность, ибо с учетом радиуса Кербола в 261600000 м мы получаем высоту над Керболом 19766012240 м, а на скриншоте немного другое число. Что ж, попробую выяснить в чём дело, а пока
Выводы
Аналогичная процедура применима к любой другой планете кербальской системы, и к любой планете Солнечной системы. Теперь мы умеем вычислять положение планет в KSP.
В следующий раз мы увидим, для чего нужны параметры ориентации плоскости орбиты в пространстве, о которых мы говорили. Наша задача научится вычислять эклиптическую долготу планеты, веть разность эклиптических долгот планеты и Кербина и есть тот самый фазовый угол, необходимый для точного расчета окна старта.
Продолжение следует...
P.S.: Небольшое исследование внутренностей KSP (законными методами, через SDK) дало понять причину неточного расчета. Дело в том что в вики даются округленные параметры орбит. Текст не переписываю, приложу только результат того же расчета но с реальными параметрами орбит

Новость отредактировал: Dunwell - 28 июл 2022 в 00:09
Hello there!
Дорогой Гость, чат доступен только для зарегистрированных пользователей.
Последние комментарии
ОБНОВЛЕНИЕ! Параллельный импорт EVE Raymarched Volumetrics версия "Иду на грозу" (июль2024)
Как сделать облака и на других планетах по типу Евы или джула. И как сделать так чтобы на дюне были
Kerbal Space Program (KSP) 1.12.5 скачать - "On Final Approach" + DLC
тут хотя бы не троян?
[РУСИФИКАТОР] KSP 1.0.x
Спасибо огромное на финальной версий 1.12.5 всё переведено идеально
Параллельный импорт EVE Raymarched Volumetrics - RSS "Облака планеты Земля"
я видеокарта gtx660 мод потянет?

ОБНОВЛЕНИЕ! Параллельный импорт EVE Raymarched Volumetrics версия "Иду на грозу" (июль2024)
доброго времени суток там случайно новых версий за полгода не вышло?

Все комментарии..
Полный список последних комментариев
Последние сообщения с форума

Все сообщения..
Полный список последних сообщений
Loading...
Нашли ошибку?
Вы можете сообщить об этом администрации.
Выделив текст нажмите Ctrl+Alt




